环形链表找入口

原题链接：142.环形链表Ⅱ

题目描述

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
注意：不能修改给定的链表

//Definition for singly-linked list
struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};

示例1：

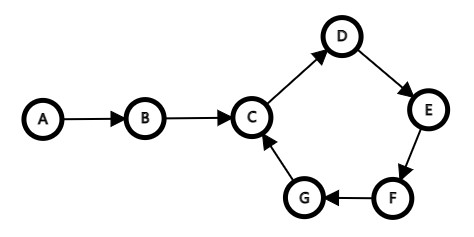
返回指向节点C的指针

示例2：

返回null

题解

方法一

　　快慢指针可用来判断链表是否存在环，基于此对其稍加修改便可得到入环的第一个节点。我们规定两个指针同时从头节点出发，慢指针每次走一个单位，而快指针每次走两个单位。若链表存在环，则二者定会相遇。当二者相遇时，将任意一个指针重新移动到头节点处，并且规定它们每次都走一个单位，再次相遇的节点即为入环的节点。这个方法的优点在于空间复杂度为$O(1)$。

证明：

　　假设我们得到了这样的一个链表：A到C需要走$m$个单位，从C出发再次到C需要走$n$个单位

　　

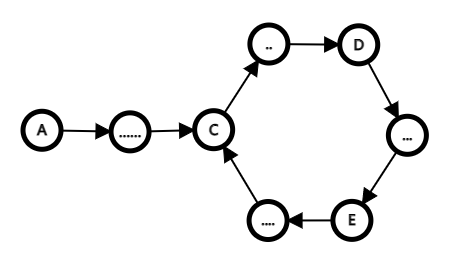
　　由方法一中的规定可知，当慢指针走到节点C，即慢指针走了$m$个单位时，快指针走了$2m$个单位，不妨假设它走到节点D。换句话说，这相当于快指针从C出发，并在环里走了$m$个单位到达了节点D，则C到D相距$m％n$个单位，因此D到C相距$n-m％n$个单位。由追及问题公式可知，从慢指针走到C时开始，还需走$\frac{追及距离}{速度差}=\frac{n-m％n}{2-1}$步二者才会相遇。不妨假设在E处快指针追上了慢指针，也就是说慢指针又走了$1 \times \frac{n-m％n}{2-1}=n-m％n$个单位到达了E，由于$n-m％n\le n $ ，可知不满一圈，故C到E相距$n-m％n$个单位，而E到C相距$m％n$个单位。然后将任意一个指针（假设是快指针）重新移动到节点A，若能证明快指针从A走到C时和慢指针再次相遇，则可说明方法一的正确性。根据规定，此时快慢指针每次都移动一个单位，故快指针还需要走$m$步到达C，因此慢指针又走了$\lfloor \frac{m}{n} \rfloor$圈以及$m％n$个单位，这等效于慢指针只走$m％n$个单位。由前文可知E到C相距$m％n$个单位，故慢指针走到了节点C，二者再次相遇，且正好为入环的节点。

代码：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *ptr1 = head;
        ListNode *ptr2 = head;
        int flag = 0;
        while(true){
            if(ptr2==NULL || ptr2->next==NULL || ptr2->next->next==NULL)
                return NULL;
            if(ptr1==ptr2 && flag==1){
                ptr1 = head;
                while(ptr1 != ptr2){
                    ptr1 = ptr1->next;
                    ptr2 = ptr2->next;
                }
                return ptr1;
            }
            if(ptr1!=ptr2 || flag==0){
                flag = 1;
                ptr1 = ptr1->next;
                ptr2 = ptr2->next->next;
                continue;
            }
        }     
    }
};

方法二

​ 我们可以对遍历的节点做记录，若当前节点已存在于记录表内，则其为入环的节点。对于记录表，可以用unordered_set来实现。

代码：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* ptr = head;
        unordered_set<ListNode*> se;
        while (true) {
            if (ptr == NULL || ptr->next == NULL) 
                return NULL;
            if (se.find(ptr) != se.end())
                return ptr; 

            se.insert(ptr);
            ptr = ptr->next;
        }
    }
};