SVM详解

本文将依次讲解Hard-Margin SVM、Soft-Margin SVM和Kernel，如果还看不懂SVM可以来🔪我

SVM简介

如何分类是机器学习中的重点，SVM便是其中一种方法，它的全称为Support vector machines，用于解决分类问题，在此我引用Machine Learning in Action by Peter Harrington 书中的原句介绍它的特点

Pros: Low generalization error, computationally inexpensive, easy to interpret results
Cons: Sensitive to tuning parameters and kernel choice; natively only handles binary classification
Works with: Numeric values, nominal values

前置知识

为了更好的阐释SVM，我需要先讲解几个重要概念

linearly separable

考虑二维空间中存在大量两种类型的点，如果我们画一条直线可以将它们分为两类，即第一种类型的点在线的一侧，第二种点则在线的另一侧，那么当这些点代表数据的时候，我们就称这些数据linearly separable。SVM能够合理分类数据，前提条件就是数据线性可分。也许你会觉得该条件有些苛刻，比如对于下面这种不太“完美”的数据，似乎无法应用SVM。

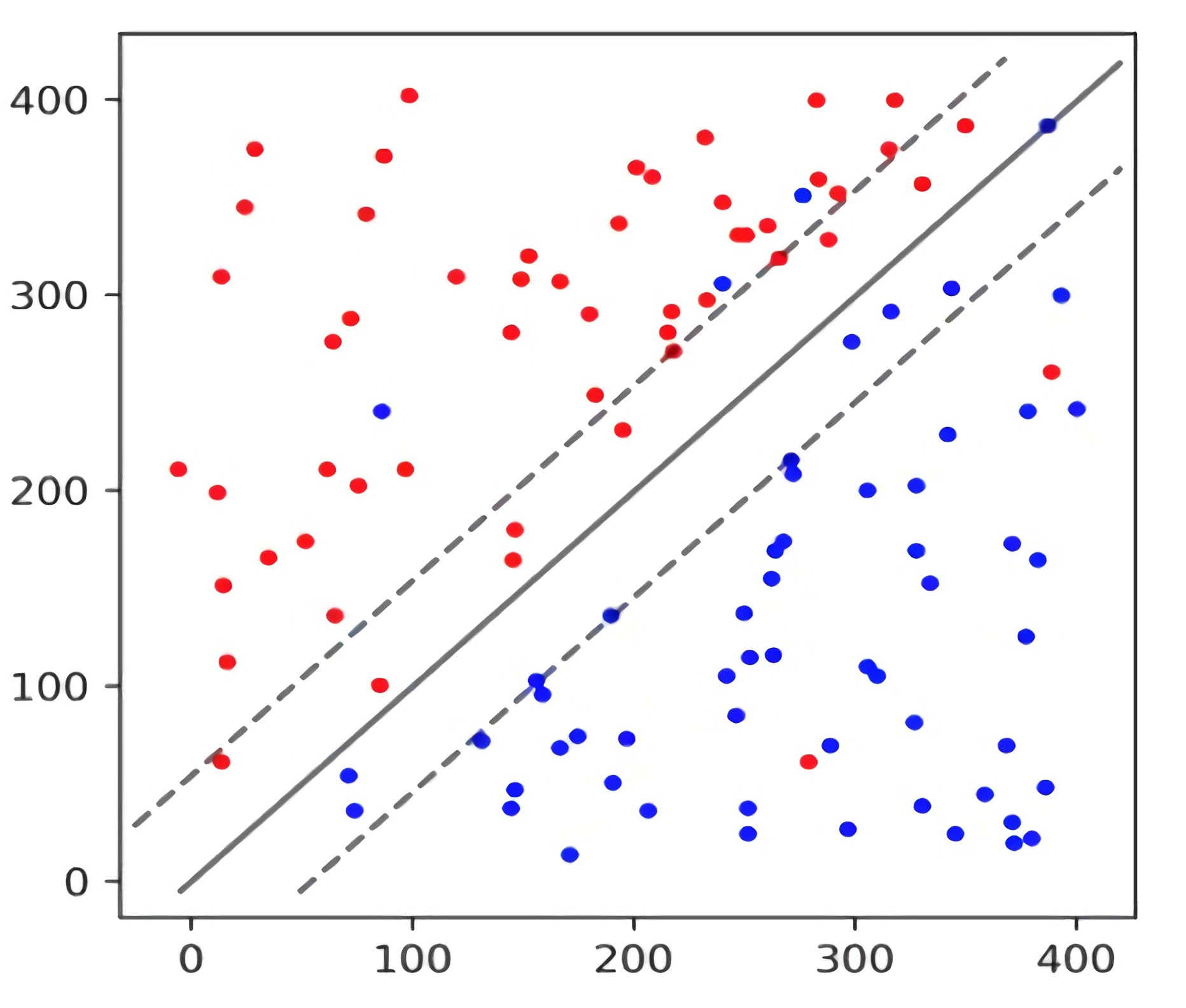
但只要我们对SVM做一些适当的升级，采用SVM Pro、SVM Pro Max 🤪，这种不完美的数据也能迎刃而解。甚至是下图这类，也不在话下。

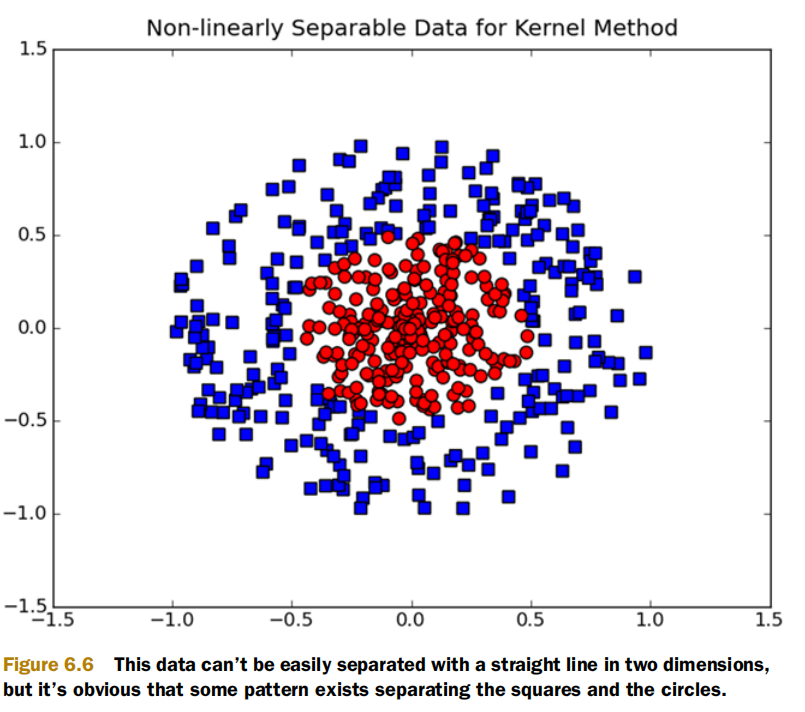
我们继续回到线性可分的问题上来，其实这条直线并不能称作线。诚然如果数据来自二维，它的表现形式的确是线，但如果数据来自三维，它的表现形式就变成了面。那么对于更高维度呢？因此这就引入了一个新的概念hyperplane。

Hyperplane

何谓超平面呢？用百度百科的话来说:

超平面是n维欧氏空间中余维度等于一的线性子空间，也就是必须是(n-1)维度。这是平面中的直线、空间中的平面之推广（n大于3才被称为“超”平面），是纯粹的数学概念，不是现实的物理概念。

超平面有一个非常漂亮的表达式
$$
\mathbf{wx}+b=0
$$
其中$\mathbf{w}$称为该超平面的法向量。你也许会问这怎么来的，既然超平面是平面中的直线、空间中的平面之推广，那我们自然就从三维空间入手。假设一个平面的法向量为$\mathbf{w}$，且该平面过定点$m=(m_1,m_2,m_3)$，那么空间中任意一点$x=(x_1,x_2,x_3)$，若它在此平面上，则必然满足
$$
\begin{aligned}
\mathbf{w}(x_1-m_1,x_2-m_2,x_3-m_3)=0\\
\mathbf{w}(\mathbf{x-m})=0\\
\mathbf{wx}+b=0
\end{aligned}
$$
其实这由面法向量与平面内的任意向量都垂直的性质可推得。因此直接推广到高维，就得到了我们想要的表达式。

值得注意的是，$\mathbf{w}$和$b$共同唯一确定一个超平面，但是对于同一个超平面，$\mathbf{w}$和$b$却不唯一。因为$\mathbf{wx}+b=0$的解也是$k\mathbf{wx}+kb=0$的解，反之亦然。故对$\mathbf{w}$和$b$同时等比例缩放，表示的还是同一超平面。这个性质在后面推导SVM公式时十分重要。

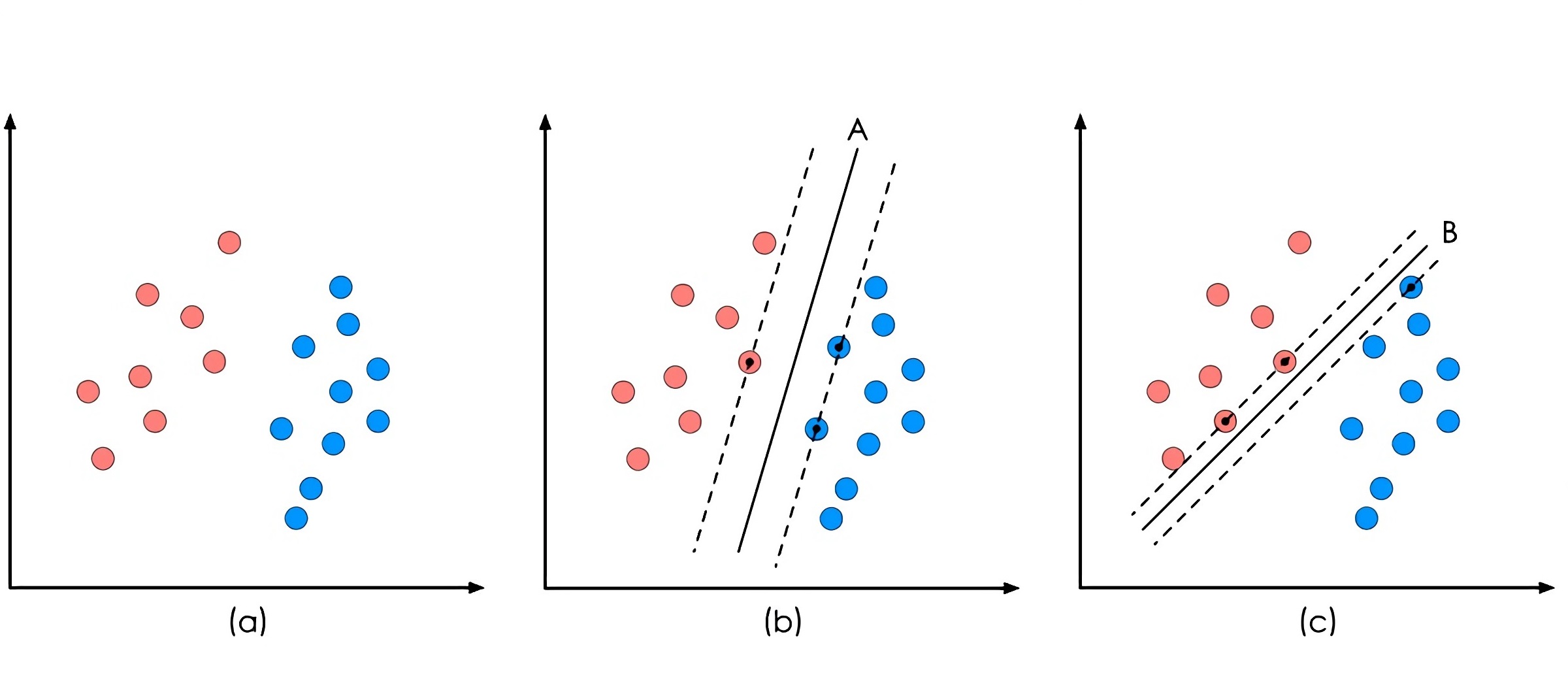
超平面是我们的决策边界，它的两侧正好表示两类数据，由训练数据得到决策边界，能够帮助我们对新的未知类型数据进行预测（分类）。可是，根据训练数据我们能够得到很多决策边界，如下图B-D

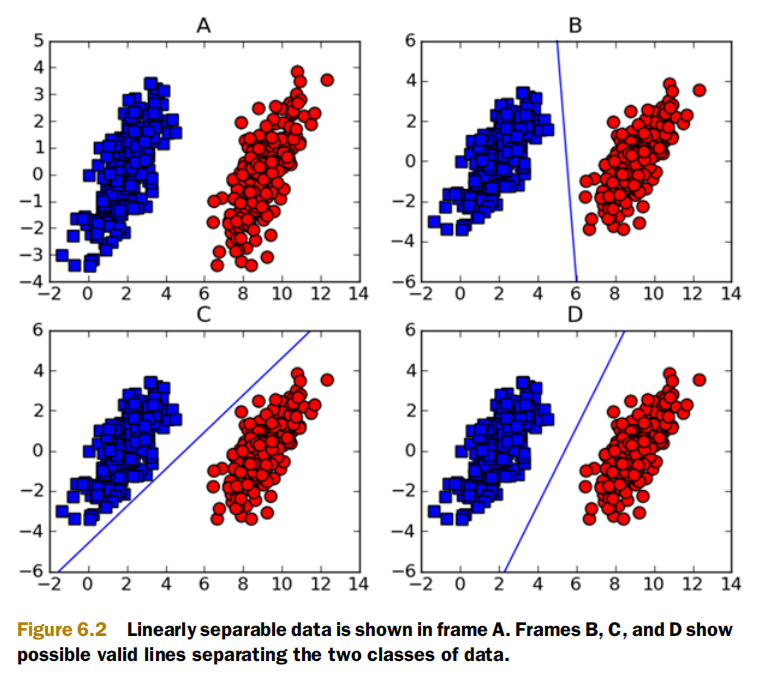
SVM将会采用哪种决策边界呢？Machine Learning in Action by Peter Harrington书中如是说到：

We’d like to find the point closest to the separating hyperplane and make sure this is as far away from the separating line as possible.

离超平面最近的点被称为support vectors，且它们到超平面的距离被称为margin。为什么我们的SVM要尽可能找最大margin的超平面？因为这样的分类器（超平面）具有很好的鲁棒性。举个栗子，我们想根据体重来判断小鼠是否长寿，于是抽样了一群小鼠，发现他们当中体重大于30g的短寿，体重小于20g的长寿，25则为具有最大margin的超平面。但由于抽样时运气不佳（没有抽到体重为26g且长寿的小鼠），真正的边界值应为28，此时我们选择的25就会比选择21好。这正是具有较好鲁棒性的体现，中庸之道🤔。

从上述的描述可以看出，SVM的算法似乎还涉及两点：点到平面的距离和求解最大值。我们来逐一了解

点$x=(x_1,\cdots,x_n)$到超平面的距离公式
$$
d=\frac{|\mathbf{wx}+b|}{||\mathbf{w}||_2}
$$
还是那句话“平面中的直线、空间中的平面之推广”，回想一下高中学过的点$(x,y)$到直线距离公式$\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$，直线的法向量为$(A,B)$，分母不正是该法向量的二范数吗？

对于求解最大值，我们需要引入新的概念——不等式约束，也许你会觉得此时的引入非常突兀，但这是求解SVM必备的知识。

不等式约束

这块知识在优化课中会重点讲解，由于笔者水平有限，其中的证明省去（以后会慢慢补上），暂时只有定理的说明。

对于如下的带约束的优化问题
$$
\begin{align}
\min\limits_{\mathbf{x}} f(\mathbf{x})&\\
s.t.g_i(\mathbf{x})&\leq 0,i=1,\cdots,m\\
h_i(\mathbf{x})&\leq 0,i=1,\cdots,m
\end{align}
$$
运用广义拉格朗日函数将带约束问题转化为无约束优化问题，即
$$
L(\mathbf{x},\lambda,\eta)=f(\mathbf{x})+\sum\limits_{i=1}^{m}\lambda_ig_i(\mathbf{x})+\sum\limits_{i=1}^{m}\eta_ih_i(\mathbf{x})
$$
令$\theta(x)=\max\limits_{\lambda\geq0,\eta}L(x,\lambda,\eta)$，此时若x在可行域，则$\theta(x)=f(x)$，原问题$\min{f(x)}$就转化成
$$
\min{f(x)}=\min\limits_{x}\theta(x)=\min\limits_{x}\max\limits_{\lambda\geq0,\eta}L(x,\lambda,\eta)
$$
可是求解$\theta_P(x)$并非易事，我们引入$\min\limits_{x}\max\limits_{\lambda\geq0,\eta}L(x,\lambda,\eta)$的对偶问题，其实就是min和max交换位置
$$
\max\limits_{\lambda\geq0,\eta}\min\limits_{x}L(x,\lambda,\eta)
$$
但$\max\min f$与$\min \max f$一定等价吗？答案为否，事实上
$$
\min\limits_{x}\max\limits_{\lambda\geq0,\eta}L(x,\lambda,\eta)\geq \max\limits_{\lambda\geq0,\eta}\min\limits_{x}L(x,\lambda,\eta)
$$
这就好比瘦死的骆驼比马大😄。不过如果满足KKT条件，那么二者可以取等！（KKT条件下次再写了💔）

到此为止前置知识全部讲解完毕，现在进入正题——SVM推导，出发！！！😎💪

SVM推导

既然是分类，我们假设class labels为+1和-1，也就是说如果数据点$\mathbf{x}$使$\mathbf{wx}+b>0$则分到+1类，小于0则分到-1类。回忆一下sigmoid函数是将数据分为0或者1，为何我们现在要把class labels给变了呢？先不急，看到后面你就会发现$\pm 1$的好处。此外，再强调一点，接下来的推导是基于训练数据线性可分，如下图所示。

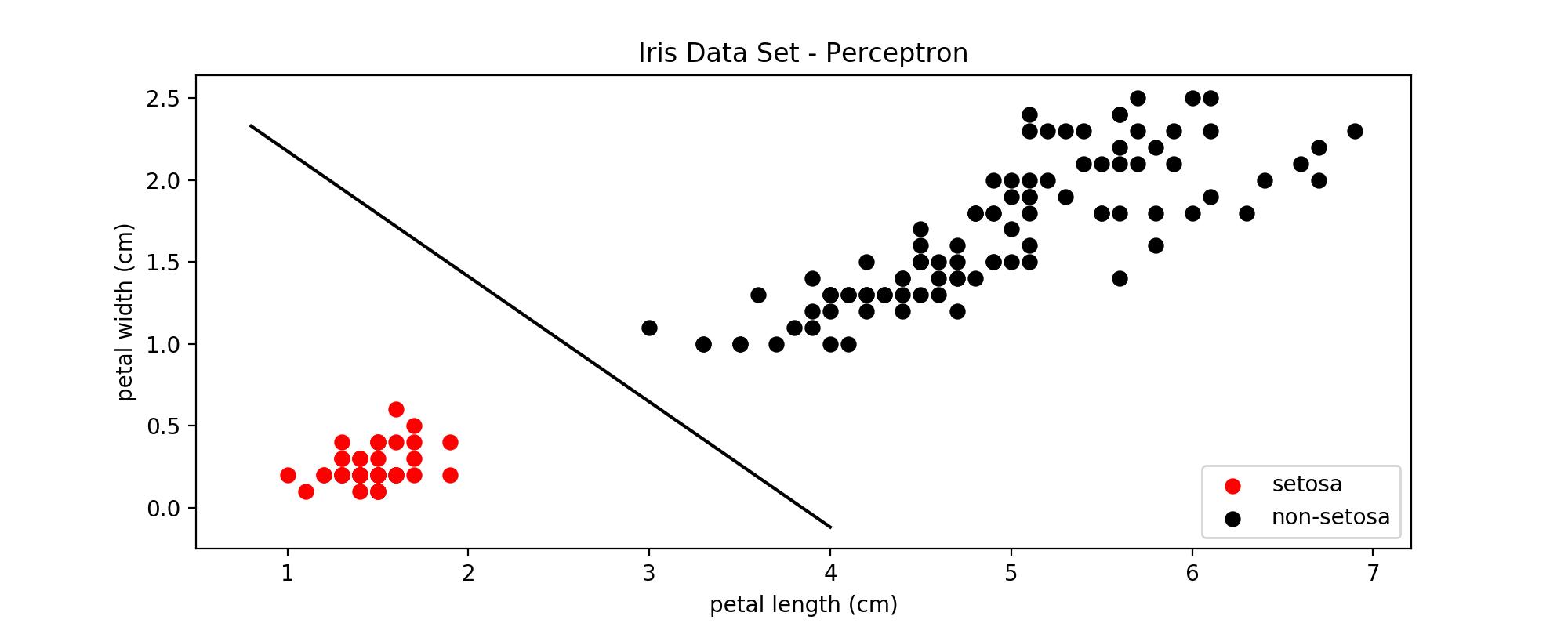
正如前文所说，我们要找最大margin的超平面，将这句话翻译成数学语言
$$
\begin{align}
&\max\limits_{\mathbf{w},b} \lambda\\
&s.t.\frac{|\mathbf{wx}_i+b|}{||\mathbf{w}||_2}\geq \lambda & i=1,\cdots,n
\end{align}
$$

$\lambda$表示的是所有点中到超平面最近的距离（点到超平面的距离公式），我们的目标就是使其尽可能的大。由于class labels为+1和-1，也就是说$y_i$要么等于1要么等于-1，并且如果数据点$\mathbf{x}$使$\mathbf{wx}+b>0$则分到+1类，此时神奇的一幕发生了，绝对值符号可以去掉
$$
\frac{|\mathbf{wx}_i+b|}{||\mathbf{w}||_2}=y_i\left (\frac{\mathbf{w}}{||\mathbf{w}||_2}\mathbf{x}_i+ \frac{b}{||\mathbf{w}||_2} \right)
$$

啊哈😏，$\pm 1$的优势尽显于此。但这个优化问题不是那么好解决，我们不得不进行转化。因为线性可分，故$\lambda$一定大于0，因此该问题可以改写为
$$
\begin{align}
&\max\limits_{\mathbf{w},b} \lambda\\
&s.t.y_i\left (\frac{\mathbf{w}}{||\mathbf{w}||_2\lambda}\mathbf{x}_i+ \frac{b}{||\mathbf{w}||_2\lambda} \right)\geq 1 & i=1,\cdots,n
\end{align}
$$

现在我们令 $\mathbf{w’}=\frac{\mathbf{w}}{||\mathbf{w}||_2\lambda}$ 以及 $b’=\frac{b}{||\mathbf{w}||_2\lambda}$ ， 前面我们讨论过，如果对 $\mathbf{w}$ 和 $b$ 同时等比例缩放，表示的还是同一超平面，因此我们解出$\mathbf{w’}$和$b’$就得到了想要的决策边界，所以上述优化问题等价于

$$
\begin{align}
&\max\limits_{\mathbf{w’},b’} \lambda\\
&s.t.y_i\left (\mathbf{w’}\mathbf{x}_i+ b’ \right)\geq 1 & i=1,\cdots,n
\end{align}
$$

不过，约束条件里都没有$\lambda$，但是目标函数里有，这解个🔨。所以我们有必要把目标函数给换了，观察$\mathbf{w’}=\frac{\mathbf{w}}{||\mathbf{w}||_2\lambda}$，可知
$$
||\mathbf{w’}||_2=\left|\left|\frac{\mathbf{w}}{||\mathbf{w}||_2\lambda}\right|\right|_2=\frac{1}{\lambda}
$$
所以$\lambda=\frac{1}{||\mathbf{w’}||_2}$，若$\lambda$想尽量大，则$||\mathbf{w’}||_2$得尽量小，继而$\frac{1}{2}||\mathbf{w’}||_2^2$也是尽量小，故原优化问题又转化成

$$
\begin{align}
&\min\limits_{\mathbf{w’},b’} \frac{1}{2}||\mathbf{w’}||_2^2\\
&s.t.y_i\left (\mathbf{w’}\mathbf{x}_i+ b’ \right)\geq 1 & i=1,\cdots,n
\end{align}
$$
注意 $y_i\left (\mathbf{w’}\mathbf{x}_i+ b’ \right)$并不是点到超平面的距离，它的值为1表示的是functional margin，一个点离超平面越远那么该乘积也会越大。而我们真正margin应为$\frac{1}{||\mathbf{w}||_2}$，下图给可以你一个直观的认识

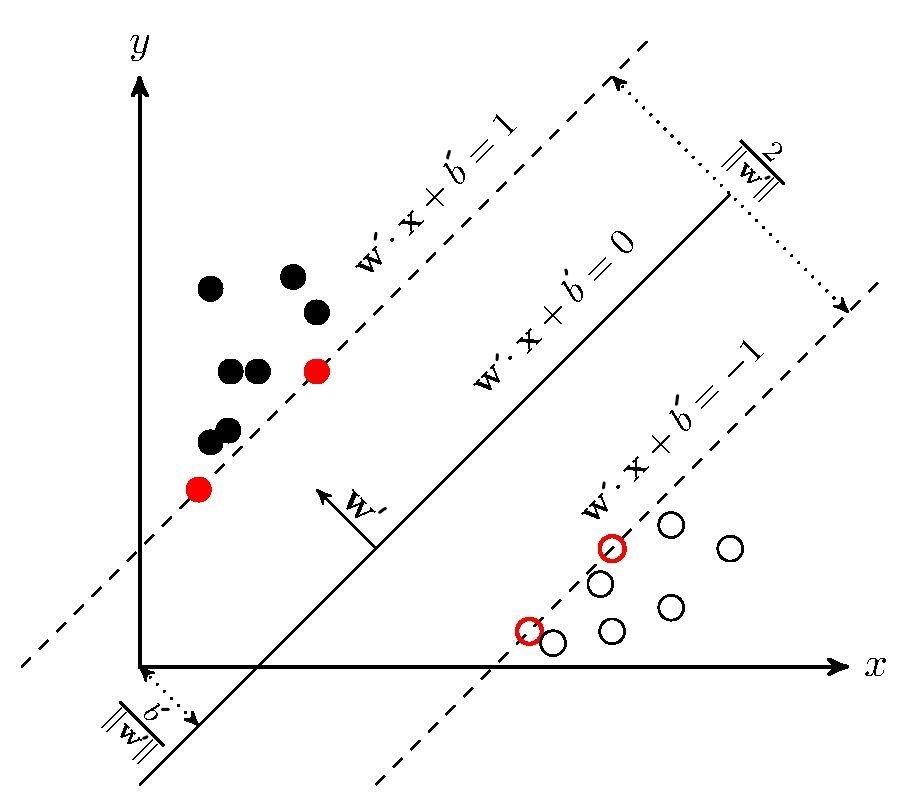
这是一个典型的不等式约束问题，所以直接利用前置知识，可得（默认$||\cdot||$为二范数）
$$
L(\mathbf{w’},b’,\alpha)=\frac{1}{2}||\mathbf{w’}||^2-\sum\limits_{i=1}^{n}\alpha_i[y_i(\mathbf{w’x}_i+b’)-1]
$$

我们要求$\min\limits_{\mathbf{w’},b’}\max\limits_{\alpha_i\geq0} L(\mathbf{w’},b’,\alpha)$，该式子中的max并不好求，怎么处理呢？还记得我们前面所说的如果满足KKT条件，则对偶问题和原问题相等。那我们就让他满足KKT条件
$$
\begin{cases}
\alpha_i \geq0 \\
y_i(\mathbf{wx}_i+b)-1 \geq 0\\
\alpha_i[y_i(\mathbf{wx}_i+b)-1]=0
\end{cases}
$$

于是求其对偶问题的解$\max\limits_{\alpha_i\geq0}\min\limits_{\mathbf{w’},b’} L(\mathbf{w’},b’,\alpha)$，对于min，我们直接令偏导为0，即

如果你记不清如何对向量求导的话，我以后会补上$\frac{\partial L}{\partial\mathbf{w’}}$该如何计算。于是我们可得

将这俩代入拉格朗日函数

至此，我们的优化问题最终转化成

SMO算法可用来求解此问题，这篇文章暂不对其进行讲解，具体的算法实现可以参考Machine Learning in Action by Peter Harrington，文末我将附上代码。解出$\boldsymbol{\alpha}$就能解出$\mathbf{w’}$，但$b’$该如何求解呢？观察KKT条件中的第三项$\alpha_i[y_i(\mathbf{wx}_i+b)-1]=0$，由于$\alpha_i \geq 0$（KKT条件第一项），所以$\alpha_i$和$y_i(\mathbf{wx}_i+b)-1$之间必有一个为0，并且如果$\boldsymbol \alpha=\mathbf{0}$，$\mathbf{w’}=\mathbf{0}$显然不成立，因此二者有且仅有一个为0。当$y_i(\mathbf{wx}_i+b)-1 \neq 0$时，$\alpha_i=0$；当$y_i(\mathbf{wx}_i+b)-1 = 0$时，$\alpha_i \neq 0$。观察图2.2，只有support vectors满足$y_i(\mathbf{w’x}+b’)-1=0$，利用该等式$b’$也就知道了。KKT条件的第三项也表明，当训练结束后，我们只需要保留support vectors，删除非support vectors并不会影响到我们的模型，因为他们的$\alpha_i=0$。

SVM升级版

不知道你是否还记得，我在linearly separable中讲到，使用SVM Pro、SVM Pro Max可以解决那些看起来不能线性可分的问题。我们先来了解SVM Pro——soft margin SVM。

soft-margin SVM

先来来看下面这张图，它和图2.2并不一样哦，多了两个”奇怪“的点

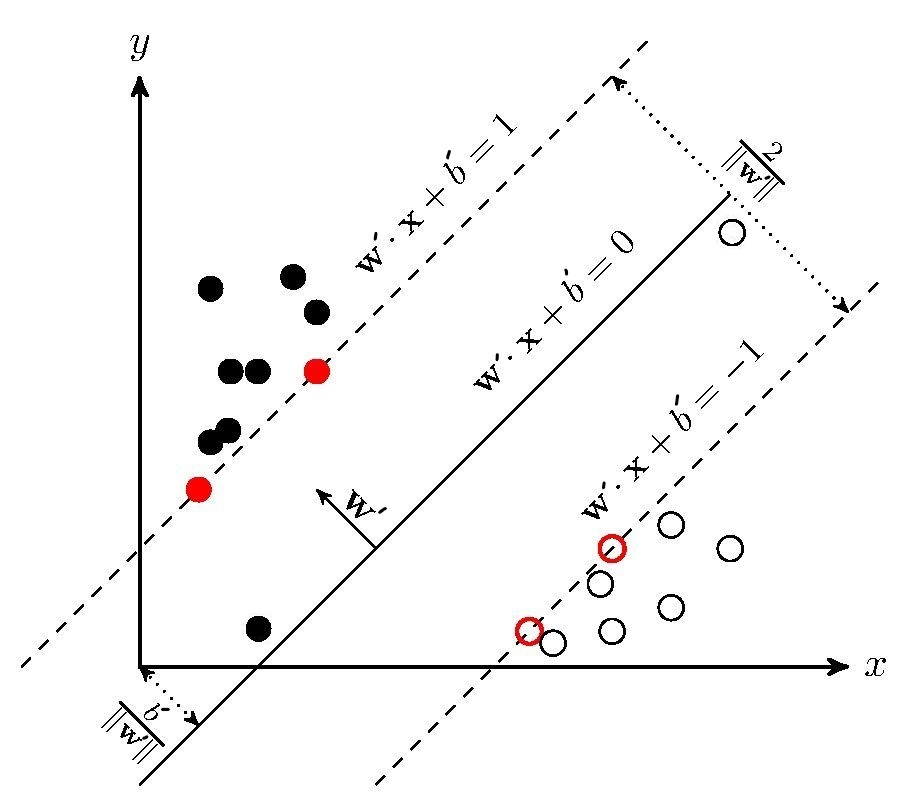
按理说，该模型训练出来的超平面并非如图所示，很明显他们各自的$y(\mathbf{w}x+b’)$都小于1，都不满足约束条件。这样的现象十分常见，毕竟数据中总会有些”不合群“的点，更有甚者会出现如下的情况——进错了家门：

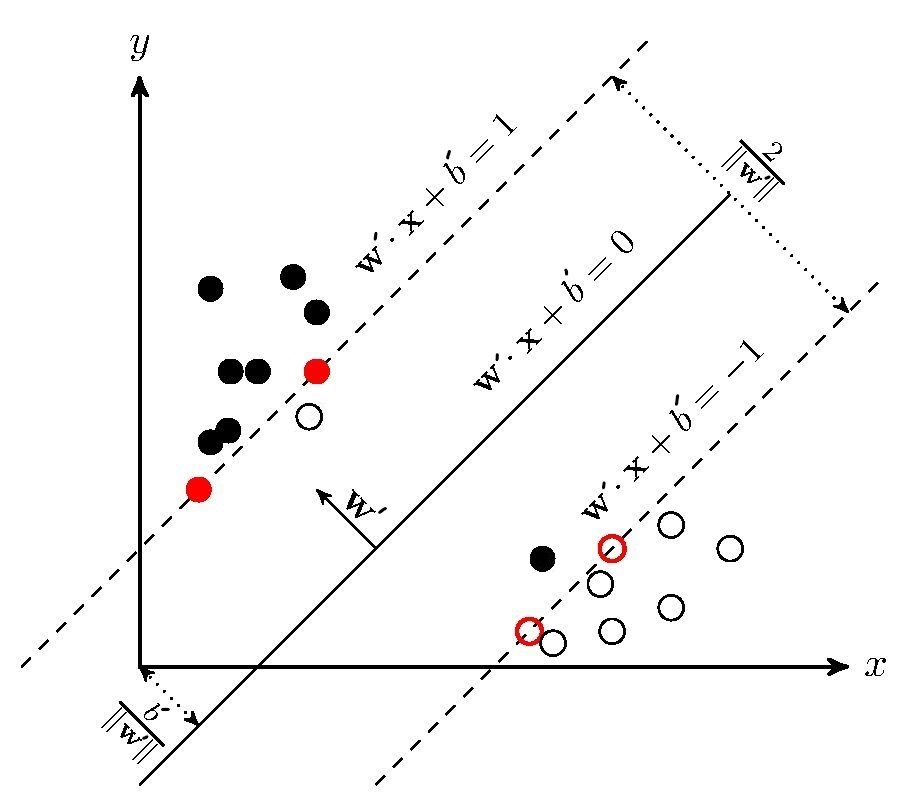
我们还是想尽量让学出来的模型和理想化的结果差不多，约束条件$\frac{|\mathbf{wx}_i+b|}{||\mathbf{w}||_2}\geq \lambda$得改造改造，允许点离超平面更近一点
$$
\frac{|\mathbf{wx}_i+b|}{||\mathbf{w}||_2}\geq \lambda-\eta_i, \eta_i\geq0
$$
在令$\xi_i=\frac{\eta_i}{\lambda}$，并且再对目标函数做一下适当的修改，否则$\eta_i$任取，那么我们的超平面就失去分类的意义了

ok，现在进入本篇最后一部分，SVM Pro Max——kernel

kernel

观察图1.2，他明明”泾渭分明“，却可惜不能用一条直线划分。很多时候，低维度不能解决的问题，但可放到高维度去解决。这就好似虚数的引入，将一维的实数数轴变成了二维的复数平面，随之而来很多问题得到了极大的简化。我们延续同样的思路——走向高维

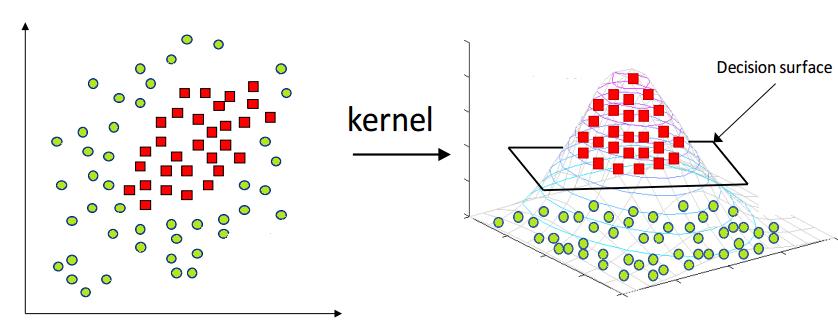
观察上图，原先二维空间下线性不可分的数据，但是到了三维就线性可分了！所以，我们需要一个映射来对数据升维，不妨用$\phi(\mathbf{x})$表示该映射关系。我们再回到SVM基础版的求解问题

自然而然，只需要把上面的$\mathbf{x}$换成$\phi(\mathbf{x})$就是现在需要求解的问题

我们的判别函数也就成了$g(\mathbf{x})=\mathbf{w}^T\phi(\mathbf{x})+b$（转置符号的出现是为了严格遵守内积的形式）但现在有个问题，$\phi(\mathbf{x}_i)^T\phi(\mathbf{x}_j)$ 为两个向量做内积，可因为升维度，计算内积会变得更加麻烦，那有没有什么方法呢？事实上我们只需要内积的值，其计算方法并不是固定。也就是说并不一定非要求出他们各自在高维的向量，然后再做内积。所以我们定义kernel function
$$
K(\mathbf{x},\mathbf{y})=\phi(\mathbf{x})^T\phi(\mathbf{y})
$$
有了核函数，$\phi$就不再需要显示的表达出来，why？因为判别函数不再需要$\phi$